Music and Sound

Music and Sound

From cymatics, to phi-ratio and Solfeggio frequencies, to Schumann Resonance, a vast amount of research into the geometries and natural harmonics of sound and music has been carried out by many people for centuries. Although it is the intention for this section to be rich with that information, in this initial launch site there is simply an exploration into some of the most fundamental cosmometric patterns found in the music system. It is only a tiny beginning of what's to come!  Tying this into the primary components of cosmometry, it becomes apparent that in essence music is a double toroidal system at its most fundamental level.


Cosmometry of Music

Although there is a vast amount of research in the arena of music and sacred geometry (which will be added as this section evolves), we’re going to begin this section simply looking at some basic patterns that tie into the fundamental components of cosmometry — the vector equilibrium and torus. This is in the context of music as a system, initially, rather than as a study of the actual frequencies and ratios inherent in that system. And it is specifically pertinent to the 12-tone tempered music scale. Again, this is a very simple initial exploration into what is a truly vast topic.

Basics of the Music System

12-Tone and 7-Tone Scales

The 12-tone musical scale consists of — you guessed it — 12 tones, or notes, labeled alphabetically as:



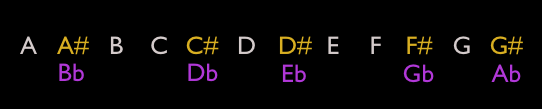
This is called the “chromatic” scale — 12 equal-interval steps up the scale (called “half steps”). As you can see, there are seven letters (A B C D E F G) and five sharps and flats (i.e. A#/Bb). The seven letters comprise the 7-note “diatonic scale” we’re all familiar with as “do, re, mi, fa, sol, la, ti…do.” In the key of C, these are C D E F G A B…C (the ending C is the beginning of the next “octave” wherein the pattern repeats at double the pitch (frequency) of the previous scale). This 7-tone scale consists of a combination of whole steps (two-note intervals) and half steps (one-note intervals) along the 12-tone chromatic scale. This 7-tone pattern is the same in all twelve keys.

Tri-Tones

Music is a system of relationships, these being the harmonic intervals between notes and the combination of these intervals to create melodies and harmonies. One of the primary interval relationships is called the tri-tone due to it being an interval of two notes that are 3 whole steps apart. Given that 3 whole steps is equal to 6 half steps, we find that these two notes exactly divide the 12-tone scale in half. As such, they can be seen as two primary “opposite” notes. In fact, the tri-tone interval, when sung or played on an instrument, is perhaps the most unresolved harmonic relationship in all of music. It is full of tension and dissonance, and yet is it present in almost every piece of music composed.

Being that the tri-tone consists of two opposite notes in the 12-tone system, it’s obvious then that there would be six pairs of these tri-tone intervals. These are colored coded in the diagram below as A/D#, A#/E, B/F, C/F#, C#/G, D/G#.




Note for later that the color coding is intentionally spectral as such: A, B, C#, D, E, F#, G# . These are the seven notes of the major scale in the key of A.

Circle of Fifths

Another very basic harmonic relationship is called the fifth. Simply, it’s the interval between the first and fifth notes of a major scale. For example, in the key of A the fifth note is E (A=1, B=2, C#=3, D=4, E=5, etc). This interval is so primary and profound in music it is actually called the “perfect fifth.” In the world of classical music theory, one of the ways to show fundamental relationships is to array the 12 notes around a circle following a sequence of fifths, as in the illustration below. This shows that there is a progression in music that naturally moves or cycles through all 12 keys in a way that is harmonically pleasing to our senses (it is also referred to as the cycle of fifths).

Using the 12-around-1 matrix pattern as our guide, the circle of 5ths looks like this (with the spectral color-coding as mentioned above):

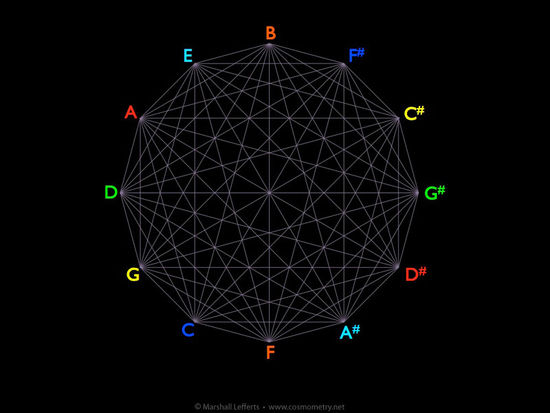
And this illustration shows that the tri-tone intervals are exactly opposite each other in the circle of fifths:

The same holds true when the 12-tone system is arrayed chromatically around the circle.

In this way we can easily see the six pairs of opposite notes that comprise the basic 12-tone system of music.

Extending this into the 3-dimensional space of the vector equilibrium, one of the primary components of cosmometry, we can map these pairs like this (notice that the circle of fifths is maintained in the sequence of notes as they are arrayed visually around the center):




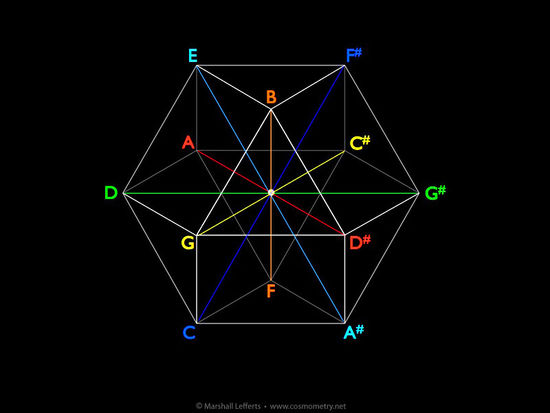
Buckminster Fuller stated that the vector equilibrium is comprised of six-pairs of equal and opposite vectors radiating from its center point. The music system aligns with that model conceptually, though of course the frequency differences of the actual tri-tone notes are not equal.

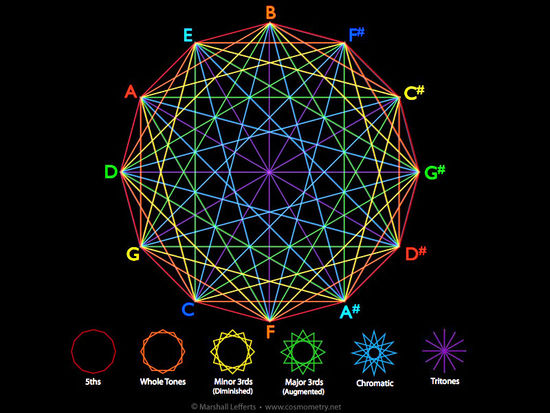
Basic Interval Polygons

With the interconnecting lines of the 12-around-1 matrix as our guide, we can then see that there is a set of basic interval relationships that map out polygonal patterns corresponding to specific intervals. As seen below, these are:


• One 12-sided dodecagon ringing the outside… our circle of fifths

• Two 6-sided hexagons… showing two sets of whole-tone (whole step) scales

• Three 4-sided squares… showing three sets of diminished (minor third) chords

• Four 3-sided triangles… showing four sets of augmented (major third) chords

• One 12-pointed dodecagram… showing the chromatic sequence of intervals

• Six lines… showing our tri-tone interval pairs

Note that the color-coding of these polygons is not coordinated with the above color-coding but is simply to make them easier to see in this illustration.





Tri-Tone Duality of Music


As seen in the Basics of the Music System article, there is a primary relationship in music (and therefore all sonic phenomena) called the tri-tone, wherein two notes are opposite each other within the 12-tone music scale. There are six pairs of these tri-tone notes altogether.

Using again the 12-around-1 matrix as our mapping tool, we’re going to see how music is based upon this tri-tone relationship at a very fundamental level.

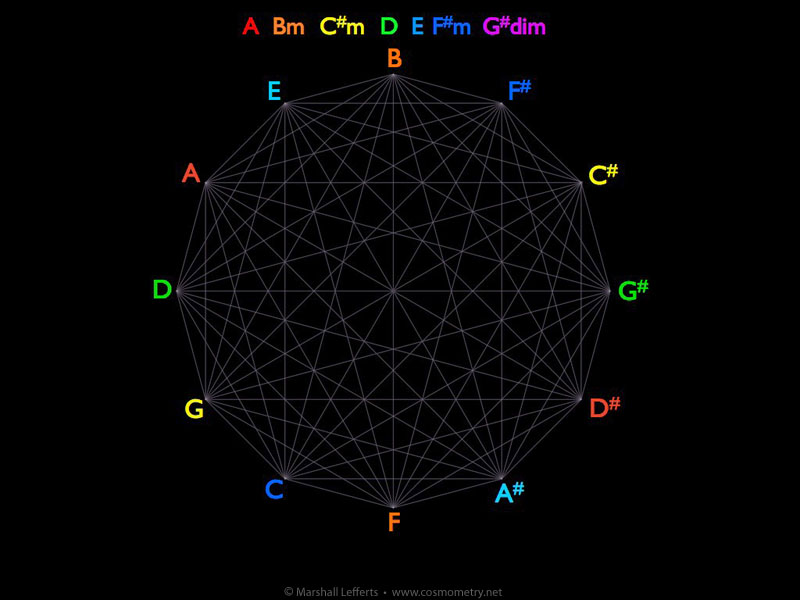
Seven Basic Triads

The familiar music scale — do, re, mi, fa, so, la, ti, do — is a seven-tone scale, with the eighth “do” completing one octave (and starting the next higher one). In the key of A, these notes are A B C# D E F# G# A. Each of these notes is the basis for a set of 3-note chords, or triads, that comprise the seven basic chords in a given key. There are three major triads (having a major third), three minor triads (having a minor third), and one diminished triad (having both a minor third and minor fifth).

In the key of A, these triads are:

A Major 1
B minor 2
C# minor 3
D Major 4
E Major 5
F# minor 6
G# diminished 7
These are also referred to numerically as the 1 chord (A Maj), 2 chord (B min), 3 chord (C# min), 4 chord (D Maj), etc, since the same pattern exists in all 12 keys and is therefore easier to speak about generically as numeric positions within the 7-tone scale.

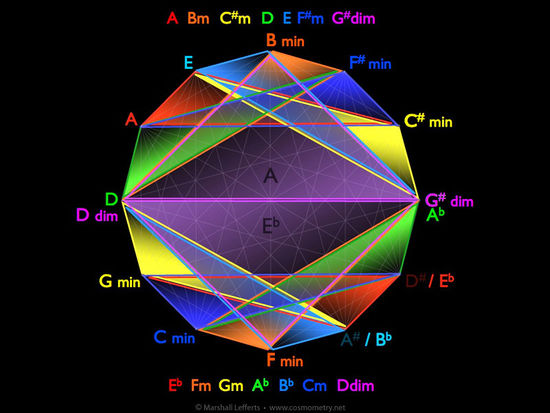
Using our color-coding spectrum, we can map out the seven triads onto our circle of fifths matrix with one colored triangle per chord. (Roll over image, then click right arrow to advance through slides, or click on icons at the bottom.)












Note the perfect symmetry of all seven chords together. This shows the innate wholeness and balance present within each key of music.


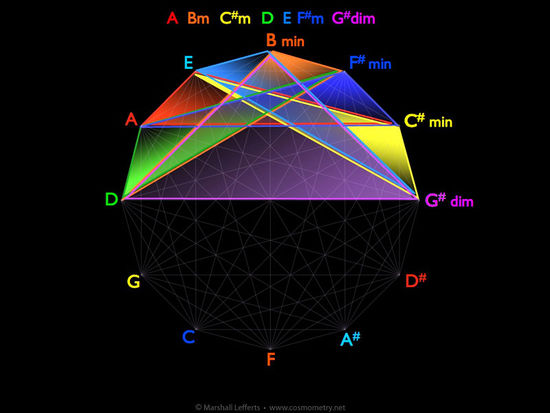
Also note that in the above image only one half of the matrix is filled in with chords. The lower half is completely empty, with five notes remaining unused. These notes are not in the key of A. They are, however in the key of D# (also known as Eb). This is the exact opposite key from A — the tri-tone key, so to speak. Eb shares two of its seven notes with A, though... the D and G# (G# is called Ab when in the key of Eb, but it's the same note). These two notes are themselves tri-tones, as evidenced by being opposite each other in the matrix. In the key of A they are the 4th and 7th notes respectively. In the key of Eb they are swapped in their positions, being the 7th and 4th notes respectively.

Adding in the triads for Eb, we get this beautiful, balanced pattern showing how it takes two opposite keys to create the whole system of music.




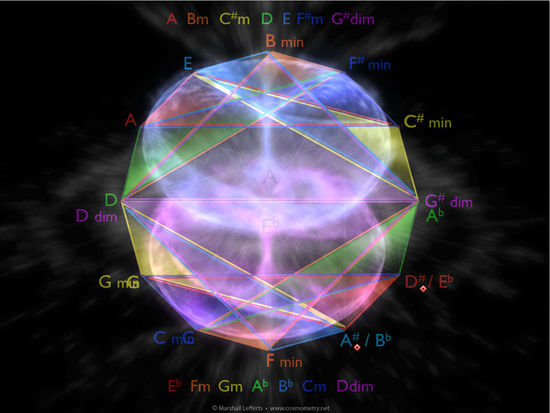
Tying this into the primary components of cosmometry, it becomes apparent that in essence music is a double toroidal system at its most fundamental level.
Bud Karas